Advection-Diffusion
Contents
Advection-Diffusion#
Python Notebooks#
Exercises:#
Task 4: Solve the Advection-Diffusion equation, with the following initial and boundary conditions: at t=0, \(c_0\)=0, for all subsequent times, c=0 at x=0, c=1 at x=L=1, u=1.0, K=0.1, and 40 grid points. Integrate over 0.05 s with a \(\Delta t\) = 0.0028 s. Plot the results and the dimensionless time scales. Increase gradually \(\Delta t\) and analyse the results. Once you understand what is happening, set again \(\Delta t\) = 0.0028 and gradually increase the wind speed. Discuss the results.
Task 5: Solve the Advection-Diffusion equation form x=0 to L, with the following initial and boundary conditions:
(11)#\[\begin{align} c(x,0)&=e^{\left(\frac{x-10}{2}\right)^2}\\ c(0,t)&=0\\ c(L,t)&=\frac{\partial c}{\partial x}=0 \end{align}\]Integrate the equation with K=0.1, u=1.0 over 0.05 s with a Δ𝑡=0.0028. Plot the results and the dimensionless time scales. Increase gradually Δ𝑡 and plot and analyze the results.
Task 6: Starting with the heat equation above simplify the equation to model the temperature evolution in the boundary layer from the surface up to H=2 km height. Assume a fair-weather condition with a subsidence of -0.001 m s\(^{-1}\). Also assume horizontal homogeneity. Parameterize the heat flux using the eddy-diffusivity closure with K=0.25 m s\(^{-2}\). Solve the simplified equation using the following initial and boundary conditions:
(12)#\[\begin{align} \theta(z,0)&=290~K\\ \overline{w'\theta'}(z,0)&=0~W~m^{-2} \\ \theta(0,t)&=290+10\cdot sin \left( \frac{2\pi \cdot t}{86400} \right) \\ \theta(H,t)&=\frac{\partial \theta}{\partial z}=0.01~K~m^{-1} \end{align}\]
What happens when you increase the subsidence to -0.01 m s\(^{-1}\)?
Plot the kinematic heat flux.
What is the maximum heat flux in W m\(^{-2}\)? Is this a realistic value for a fair-weather condition?
Calculate the heating rate in K per hour.
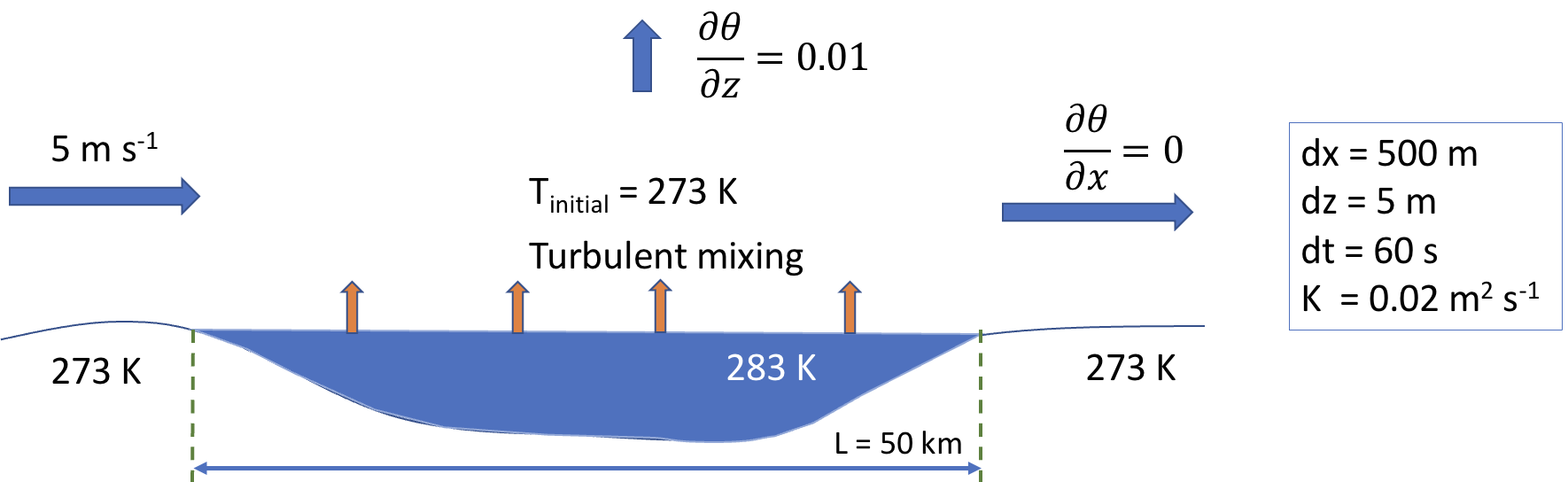
Task 7: Intense boundary layer convection may develop when cold air masses are advected over relatively warm surfaces. Develop a simple model for this by assuming that the time evolution of the boundary layer is determined by the vertical turbulent heat transport and the horizontal heat advection. Make the following assumptions: [Hint: use the eddy-diffusivity closure and the upwind scheme for the advection flux]
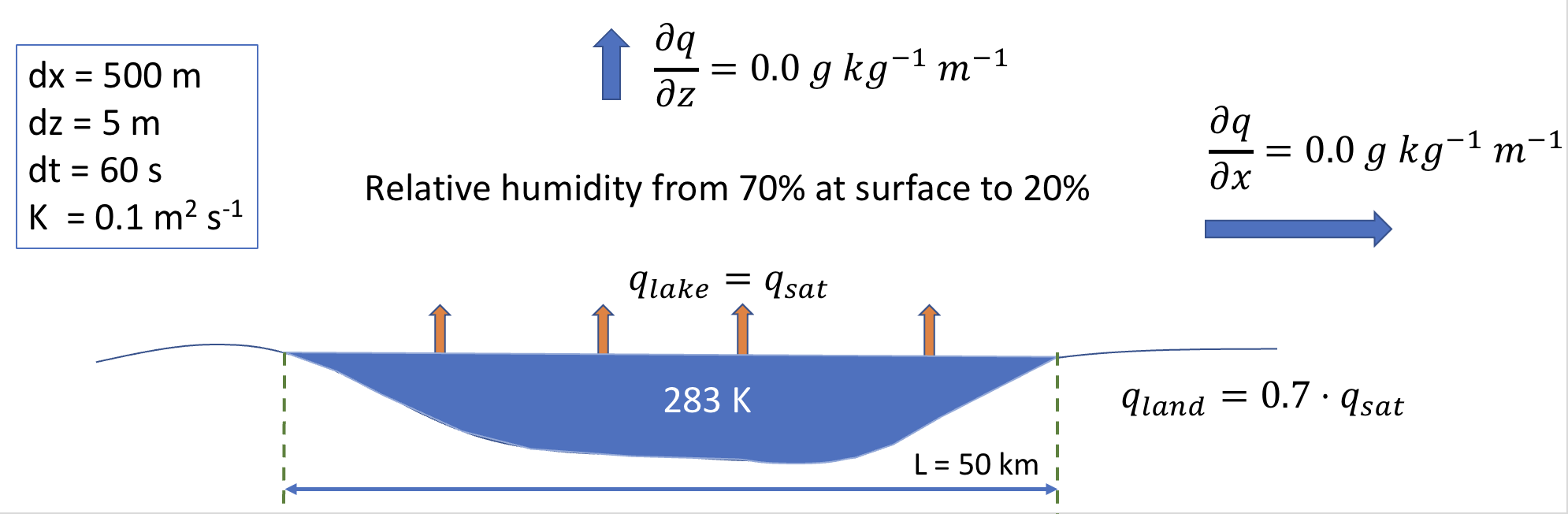
Task 8: Extend the Lake-effect model by adding the moisture transport equation. Assume that the top millimetres above the water surface are saturated. Assume that the relative humidity in the atmosphere decreases linearly from 70 to 20 %. Calculate the relative humidity at each grid cell to identify where condensation takes place [Note: Convert the potential temperature to normal temperature (by adding a lapse rate) and calculate the mixing ratio at each cell. Then calculate the relative humidity.]