Fluid dynamics#

Exercises:#

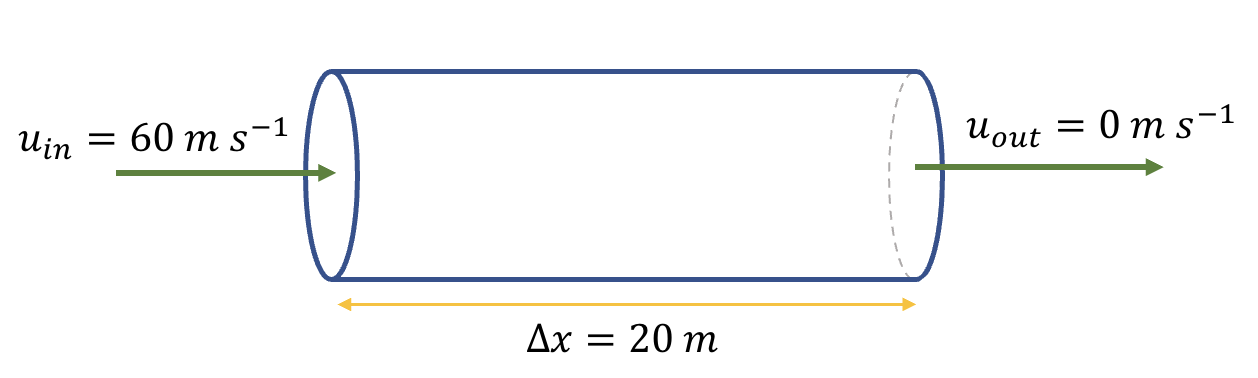
Task 1: Hurricane-force winds of 60 m s\(^{–1}\) blow into an west-facing entrance of a 20 m long pedestrian tunnel. The door at the other end of the tunnel is closed. The initial air density in the tunnel is 1.2 kg m\(^{–3}\). Find the rate of air density increase in the tunnel.

../_images/exercise_mass_conservation.png

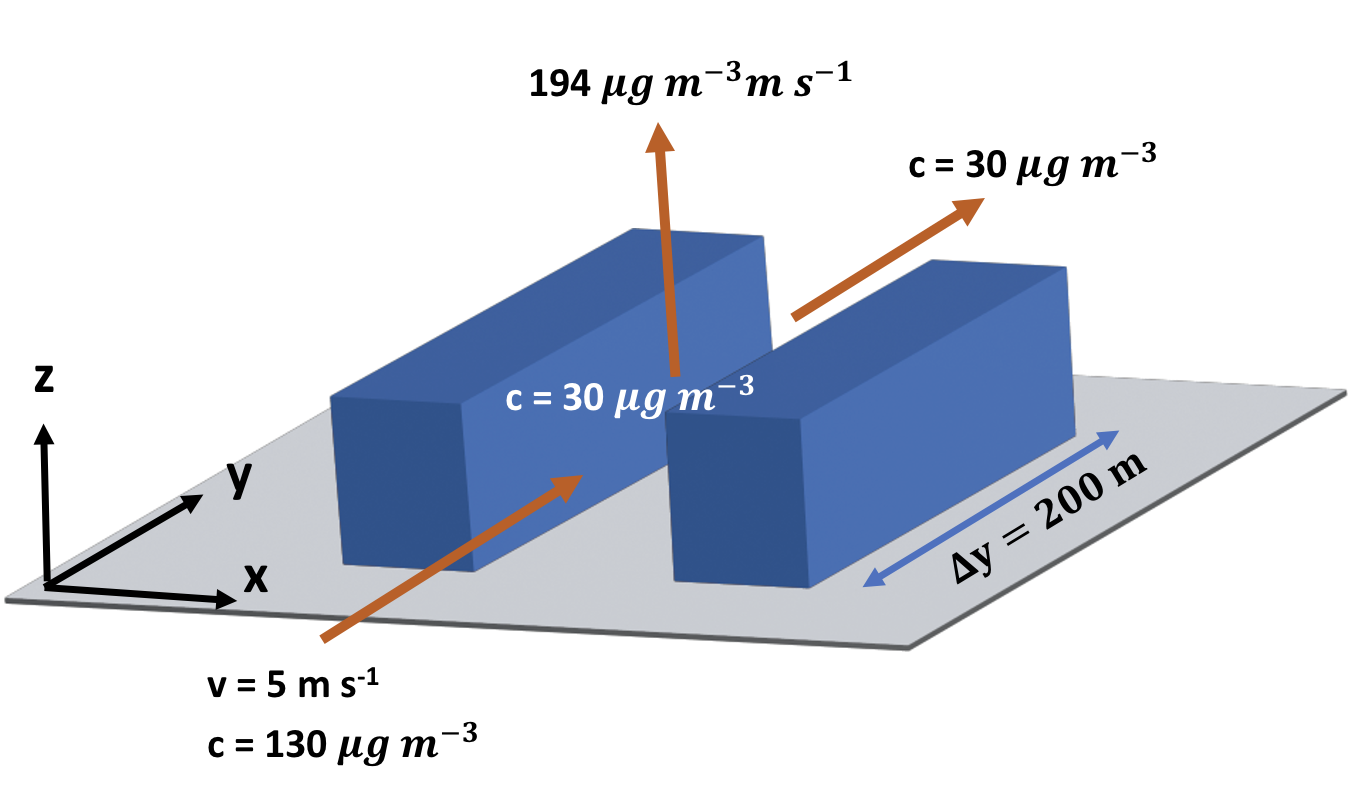
Task 2: In a narrow street canyon, a fine particle matter load of 30 \(\mu g \cdot m^{−3}\) is measured. A moderate wind blows from the south, advecting further particles from a busy road. The concentration at the road is 130 \(\mu g \cdot m^{-3}\). Turbulent mixing causes 194 \(\mu g \cdot m \cdot s^{-1}\) to be entrained upwards. Does the concentration exceed the critical threshold value of 150 \(\mu g \cdot m^{-3}\) after one hour?

../_images/street_canyon.png

Task 3: The cube of air below has \(\theta\) = 12°C along its south side, but smoothly increases in temperature to 15°C on the north side. This 100 km square cube is advecting toward the north at 25 km/hour. What warming rate at a fixed thermometer can be attributed to temperature advection?

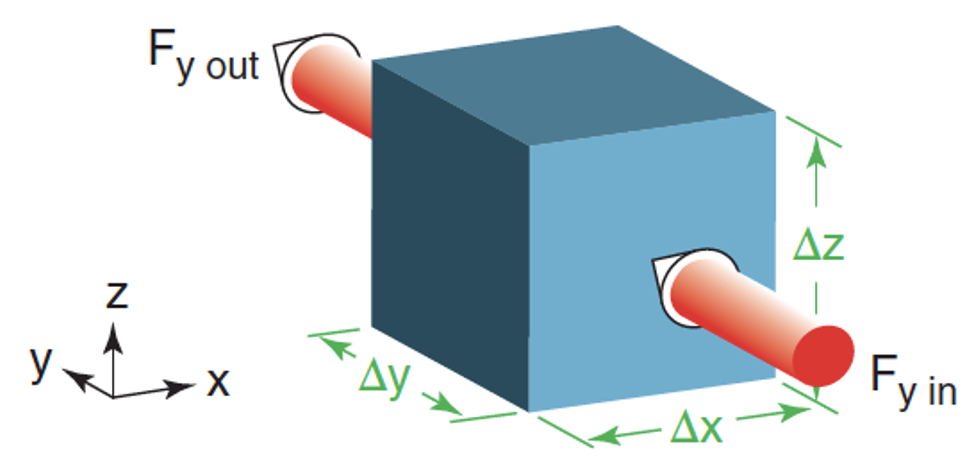
../_images/cube.png

Task 4:In the figure above (Task 3), suppose that the incoming heat flux from the south is 5 W m\(^{–2}\), and the outgoing on the north face of the cube is 7 W m\(^{–2}\).

  1. Convert these fluxes to kinematic units.

  2. What is the value of the kinematic flux gradient?

  3. Calculate the warming rate of air in the cube, assuming the cube has zero humidity and is at a fixed altitude where air density is 1 kg m\(^{–3}\). The cube of air is 10 m on each side.

Task 5: Bremen is about 600 km north of Stuttgart. In Bremen the wind components (U, V) are (6, 4) m s\(^{–1}\) , while in Stuttgart they are (2, 10) m s\(^{–1}\). What is the value of the advective force per mass?

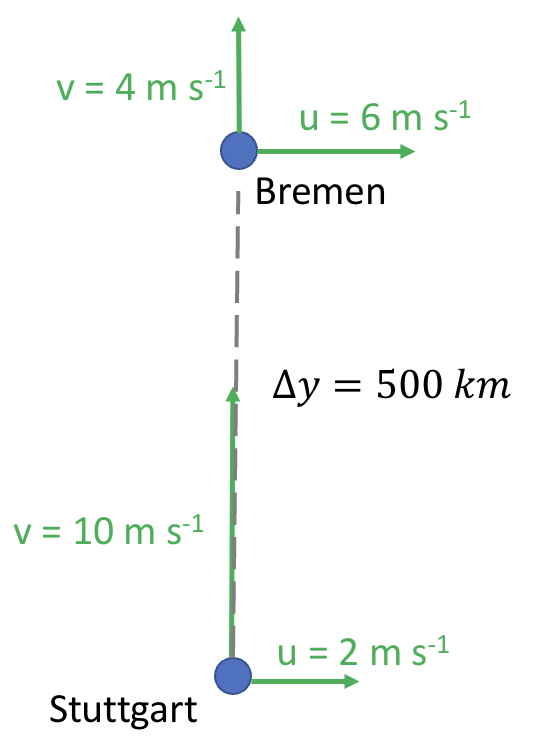
../_images/bremen_stuttgart.png

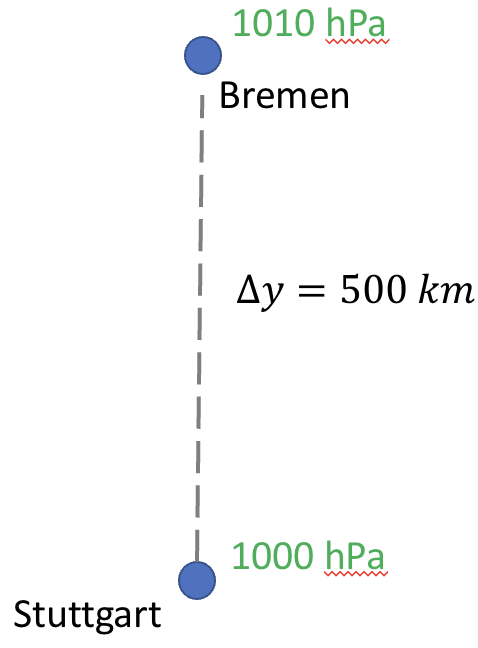
Task 6: Bremen is about 600 km north of Stuttgart. In Bremen the pressure is 1010 hPa, while in Stuttgart the pressure is 1000 hPa. Find the pressure gradient force? (let \(\rho\) = 1.1 kg m\(^{-3}\))

../_images/bremen_stuttgart_2.png

Homework:#

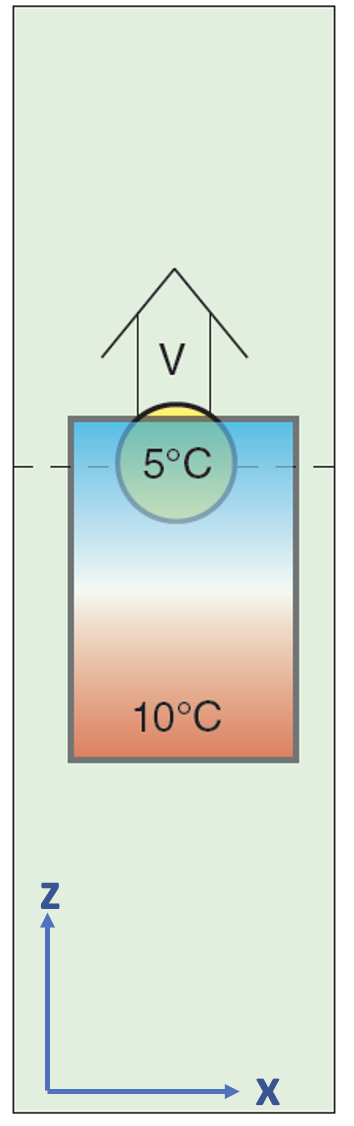
Homework 1: Given the figure below, assume that higher in the figure corresponds to higher in the atmosphere. Suppose that the 5°C air is at a relative altitude that is 500 m higher than that of the 10°C air. If the updraft is 500 m/(10 hours), what is the temperature at the thermometer (yellow circle) after 10 hours?

../_images/homework_vertical_advection.png

Homework 2: The potential temperature of the air increases 5°C per 100 km distance east. If an east wind of 20 m s\(^{–1}\) is blowing, find the advective flux gradient, and the temperature change associated with this advection.

Homework 3: Suppose that the turbulent heat flux decreases linearly with height according to \(\overline{w'\theta'}=a-b \cdot z\), where a = 0.3 (K ms\(^{-1}\)) and b = \(3 \cdot 10^{−4}\) (K s\(^{-1}\)). If the initial temperature profile is an arbitrary shape, then what will be the shape of the final profile on hour later? Neglecting subsidence, radiation, latent heating, and assume horizontal heterogeneity.

Homework 4: If a horizontal wind of 10 m/s is advecting drier air into a region, where the horizontal moisture gradient is (5 g\(_{water}\)/kg\(_{air}\))/100 km, then what vertical gradient of turbulent moisture flux in the boundary layer is required to maintain a steady-state specific humidity? Assume there is no body source of moisture.

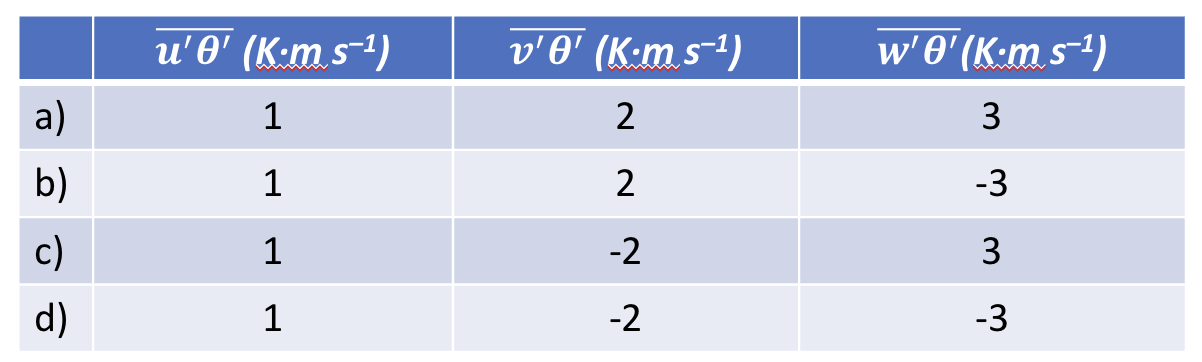
Homework 5: : Find the rate of temperature change (°C h\(^{–1}\)) with no internal heat source, given the kinematic flux divergence values below. Assume \(\Delta x = \Delta y = \Delta z = 1\) km.

../_images/table_fluid_1.png

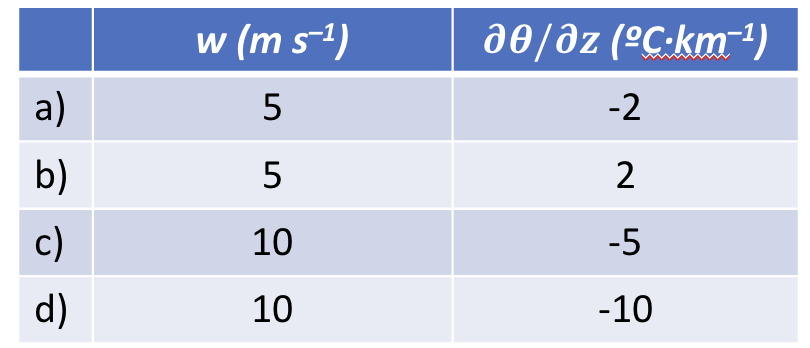
Homework 6: Given the wind and temperature gradient, find the value of the kinematic advective flux gradient (°C h\(^{–1}\)).

../_images/table_fluid_2.png