Boundary layer model with coupled surface energy balance and soil module
Boundary layer model with coupled surface energy balance and soil module#
The aim of this exercise is to include the SEB and soil module in the boundary layer model.
Step 1: Load the SEB model.
import math
import numpy as np
from scipy.optimize import minimize, minimize_scalar
import matplotlib.pyplot as plt
%matplotlib inline
def EB_fluxes(T_0,T_a,f,albedo,G,p,rho,U_L,z,z_0):
""" This function calculates the energy fluxes from the following quantities:
Input:
T_0 : Surface temperature, which is optimized [K]
f : Relative humdity as fraction, e.g. 0.7 [-]
albedo : Snow albedo [-]
G : Shortwave radiation [W m^-2]
p : Air pressure [hPa]
rho : Air denisty [kg m^-3]
z : Measurement height [m]
z_0 : Roughness length [m]
"""
# Some constants
c_p = 1004.0 # specific heat [J kg^-1 K^-1]
kappa = 0.40 # Von Karman constant [-]
sigma = 5.67e-8 # Stefan-Bolzmann constant
# Bulk coefficients
Cs_t = np.power(kappa,2.0) / ( np.log(z/z_0) * np.log(z/z_0) )
Cs_q = np.power(kappa,2.0) / ( np.log(z/z_0) * np.log(z/z_0) )
# Correction factor for incoming longwave radiation
eps_cs = 0.23 + 0.433 * np.power(100*(f*E_sat(T_a))/T_a,1.0/8.0)
# Select the appropriate latent heat constant
L = 2.83e6 # latent heat for sublimation
# Calculate turbulent fluxes
H_0 = rho * c_p * Cs_t * U_L * (T_0-T_a)
E_0 = rho * ((L*0.622)/p) * Cs_q * U_L * (E_sat(T_0)-f*E_sat(T_a))
# Calculate radiation budget
L_d = eps_cs * sigma * (T_a)**4
L_u = sigma * (T_0)**4
Q_0 = (1-albedo)*G #+ L_d - L_u
return (Q_0, L_d, L_u, H_0, E_0)
def E_sat(T):
""" Saturation water vapor equation """
Ew = 6.112 * np.exp((17.67*(T-273.16)) / ((T-29.66)))
return Ew
def optim_T0(x,T_a,f,albedo,G,p,rho,U_L,z,z0):
""" Optimization function for surface temperature:
Input:
T_0 : Surface temperature, which is optimized [K]
f : Relative humdity as fraction, e.g. 0.7 [-]
albedo : Snow albedo [-]
G : Shortwave radiation [W m^-2]
p : Air pressure [hPa]
rho : Air denisty [kg m^-3]
z : Measurement height [m]
z_0 : Roughness length [m]
"""
Q_0, L_d, L_u, H_0, E_0 = EB_fluxes(x,T_a,f,albedo,G,p,rho,U_L,z,z0)
# Get residual for optimization
res = np.abs(Q_0+L_d-L_u-H_0-E_0)
# return the residuals
return res
Step 2: Extend the heat equation to 2D.
import numpy as np
import matplotlib.pyplot as plt
import math
def heat_equation_time_2D(T, dz, dt):
""" This is a 2D version of the heat equation. It takes an initial 2D-temperature
field, dz the spacing in the vertical and the timestep dt. The function returns the
updated temperature field.
T :: Initial temperature field [K]
dz :: Grid spacing in z-direction [m]
dt :: Timestep [s]
"""
# Definitions and assignments
K = 1.2e-6 # Thermal conductivity
# Define index arrays (z-direction)
Nz = T.shape[0]
k = np.arange(1,Nz-1) # all indices at location i
kr = np.arange(2,Nz) # all indices at location i+1
kl = np.arange(0,Nz-2) # all indices at location i-1
# Create array for new temperature values
Tnew = T
# Loop over x-direction
for x in range(T.shape[1]):
# Set lower BC - Neumann condition
T[Nz-1,:] = T[Nz-2,:]
# Update temperature using indices arrays
Tnew[k,x] = T[k,x] + ((T[kr,x] + T[kl,x] - 2*T[k,x])/dz**2) * dt * K
# Copy the new temperature as old timestep values (used for the
# next time loop step)
T = Tnew
# return temperature array, grid spacing, and number of integration steps
return T
Step 3: Test the soil module
# Define necessary variables and parameters
# for the soil module
Nx = 20
Nz = 40
dx = 500
dz = 0.5
x = np.arange(0, Nx*dx, dx)
z = np.arange(0, -Nz*dz, -dz)
# Initial temperature field
T = np.zeros((Nz, Nx))
# Do some test runs
for t in range(4):
T = heat_equation_time_2D(T, 1, 86400)
plt.figure(figsize=(15,6))
plt.contourf(x, z, T);

Step 4: Add the boundary layer model.
import numpy as np
import matplotlib.pyplot as plt
import math
# --------------------------
# Auxiliary functions
# --------------------------
def saturation_water_vapor(T):
""" Calculates the saturation water vapor pressure [Pa]"""
return ( 6.122*np.exp( (17.67*(T-273.16))/(T-29.66) ) )
def hypsometric_eqn(p0, Tv, z):
"""Hypsometric equation to calculate the pressure [hPa] at a certain height[m]
when the surface pressure is given
p0 :: surface pressure [hPa]
Tv :: mean virtual temperature of atmosphere [K]
z :: height above ground [m]
"""
return(p0/(np.exp((9.81*z)/(287.4*Tv) )))
def mixing_ratio(theta, p0, Tv, z):
""" Calculates the mixing ratio from
theta :: temperature [K]
p0 :: surface pressure [hPa]
Tv :: mean virtual temperature of atmosphere [K]
z :: height [m]
"""
return(622.97 * (saturation_water_vapor(theta)/(hypsometric_eqn(p0,Tv,z)-saturation_water_vapor(theta))))
def make_plot(data, x, z, levels, title, unit, xlab, zlab, cmap='RdBu_r', size=(18,5)):
""" Useful function for plotting 2D-fields as contour plot"""
# Create figure
fig, ax = plt.subplots(1,1,figsize=size);
cn0 = ax.contourf(x,z,data,10,origin='lower',levels=levels,cmap=cmap);
# Add the colorbar and set ticks and labels
cbar= fig.colorbar(cn0, ax=ax, orientation='vertical')
cbar.set_label(label=unit, size=16)
cbar.ax.tick_params(labelsize=14)
# Add labels and modify ticks
ax.set_xlabel(xlab, fontsize=14)
ax.set_ylabel(zlab, fontsize=14)
ax.set_title(title)
# return the handler to the figure axes
return ax
def boundary_layer_evolution_moisture(theta, q, u, K, dx, dz, Nx, Nz, dt):
""" Simple advection-diffusion equation for temperature and moisture.
theta :: Initial temperature field [K]
q :: Initial moisture field [g/kg]
u :: Fluid velocity [m/s]
K :: turbulent diffusivity [m^2/s]
dx :: Grid spacing in x-direction [-]
dz :: Grid spacing in z-direction [-]
Nx :: Number of grid cells in x-direction [m]
Nz :: Number of grid cells in z-direction [m]
dt :: time step in seconds [s]
"""
# Define index arrays
# Since this a 2D problem we need to define two index arrays.
# The first set of index arrays is used for indexing in x-direction. This
# is needed to calculate the derivatives in x-direction (advection)
k = np.arange(1,Nx-1) # center cell
kr = np.arange(2,Nx) # cells to the right
kl = np.arange(0,Nx-2) # cells to the left
# The second set of index arrays is used for indexing in z-direction. This
# is needed to calculate the derivates in z-direction (turbulent diffusion)
m = np.arange(1,Nz-1) # center cell
mu = np.arange(2,Nz) # cells above
md = np.arange(0,Nz-2) # cells below
# --------------------------
# Init other arrays
# --------------------------
cov = np.zeros((Nz, Nx)) # Empty array for the covariances
adv = np.zeros((Nz, Nx)) # Empty array for the advection term
# --------------------------
# Dimensionless parameters
# --------------------------
c = (u*dt)/dx
d = (K*dt)/(dz**2)
# --------------------------
# Integrate the model
# --------------------------
# Note, not time iteration since this model only updates the temperature field
# for one timestep using dt
# Set BC top (Neumann condition)
# The last term accounts for the fixed gradient of 0.01
theta[Nz-1, :] = theta[Nz-2, :]
# Set top BC for moisture
q[Nz-1, :] = q[Nz-2, :]
# Set BC right (Dirichlet condition)
theta[:, Nx-1] = theta[:, Nx-2]
# Set right BC for moisture
q[:, Nx-1] = q[:, Nx-2]
# We need to keep track of the old values for calculating the new derivatives.
# That means, the temperature value a grid cell is calculated from its values
# plus the correction term calculated from the old values. This guarantees that
# the gradients for the x an z direction are based on the same old values.
old = theta
old_q = q
# First update grid cells in z-direction. Here, we loop over all x grid cells and
# use the index arrays m, mu, md to calculate the gradients for the
# turbulent diffusion (which only depends on z)
for x in range(1,Nx-1):
# Update temperature including lapse rate
theta[m,x] = theta[m,x] + ((K*dt)/(dz**2))*(old[mu,x]+old[md,x]-2*old[m,x]) + lapse_rate
# Moisture transport (turbulent diffusion)
q[m,x] = q[m,x] + ((K*dt)/(dz**2))*(old_q[mu,x]+old_q[md,x]-2*old_q[m,x])
# Calculate the warming rate [K/s] by covariance
cov[m,x] = ((K)/(dz**2))*(old[mu,x]+old[md,x]-2*old[m,x])
# Then update grid cells in x-direction. Here, we loop over all z grid cells and
# use the index arrays k, kl, kr to calculate the gradients for the
# advection (which only depends on x)
for z in range(1,Nz-1):
# temperature advection
theta[z,k] = theta[z,k] - ((u*dt)/(dx))*(old[z,k]-old[z,kl])
# moisture advection
q[z,k] = q[z,k] - ((u*dt)/(dx))*(old_q[z,k]-old_q[z,kl])
# Calculate the warming rate [K/s] by the horizontal advection
# Note: Here, we use a so-called upwind-scheme (backward discretization)
adv[z,k] = - (u/dx)*(old[z,k]-old[z,kl])
# Calculate new saturation mixing ratio
qsat = mixing_ratio(theta, 1013, 270, height)
# Then the relative humidity using qsat
# Limit the relative humidity to 100 %
rH = np.minimum(q/qsat, 1)
# Return results
return theta, q, qsat, rH, cov, adv, c, d, np.arange(0, Nx*dx, dx), np.arange(0, Nz*dz, dz)
Step 5: Combine the boundary layer model with the SEB and soil modules.
#--------------------------------------------
# General parameters
#--------------------------------------------
lake_from = 10 # Where does the lake start (grid cell)
lake_to = 20 # where does the lake end (grid cell)
Nx = 50 # how many grid cells in x-direction
dx = 500 # grid spacing in x
# Integration parameters
dt = 60 # timestep in seconds
integration = 4*60 # number of integration steps
#--------------------------------------------
# Define necessary variables and parameters
# for the SEB
#--------------------------------------------
albedo = 0.3 # albedo [-]
G = 200.0 # Incoming shortwave radiation
rho = 1.1 # Air density [kg m^-3]
U = 5.0 # Wind velocity [m/s]
z = 2.0 # Measurement height [m]
z0 = 1e-3 # Roughness length [m]
p = 1013 # Pressure [hPa]
#--------------------------------------------
# Define necessary variables and parameters
# for the soil module
#--------------------------------------------
Nz = 10 # Number of grid cells in the soil
dz = 0.1 # grid spacing [m]
Tsoil = 268 # Initial soil temperatures
Tlake = 278 # Lake temperatures
# Initial soil temperature field
T = Tsoil * np.ones((Nz, Nx))
T[:, lake_from:lake_to] = Tlake
# --------------------------------------
# Initial atmospheric temperature field
# --------------------------------------
Nza = 20 # Number of vertical grid cells in the atmosphere
dza = 10 # Grid spacing [m]
# Neutral stratification with lapse rate of 0.01 K/m
# Create a 1D-array with the vertical temperature distribution
# Surface = 268 K, decreasing according to the dry-adiabative lapse rate 0.01 K/m
Tatm = 268 # initial temperature of the atmosphere [K]
lapse_rate = -0.01 # lapse rate [K/m]
theta_vec = np.array([Tatm + lapse_rate * (dza * z) for z in range(Nza)])
theta = np.array([theta_vec,] * Nx).transpose()
# The lower temperature boundary needs to be updated where there is the lake
theta[0, lake_from:lake_to] = Tlake
# Make height grid
height = np.array([np.arange(0,Nza*dza,dza),] * Nx).transpose()
# --------------------------
# Initialize moisture fields
# --------------------------
# Init saturation mixing ratio array
qsat = mixing_ratio(theta, 1013, Tatm, height)
# Use qsat to derive mixing ratio at each grid cell assuming a
# decreasing relative humidity from 70 % at the surfacee to 20 % at the top
q = (qsat.T * np.linspace(0.8, 0.2, Nza)).T
# The lower moisture boundary needs to be updated where there is the lake
# Here, were set the moisture at the lower boundary from the grid cell 50
# to 150 to a mixing ratio of 0.9 times the saturation mixing ratio
q[0, lake_from:lake_to] = 0.95 * qsat[0, lake_from:lake_to]
# Iterate over time
for t in range(integration):
# Loop over all x-cells and calculate the surface temperature
for x in range(T.shape[1]):
# Keep the same temperature for the lake (no heating)
if (x>=lake_from) & (x<=lake_to):
T[0,x] = Tlake
else:
# Set the initial guess for the temperature optimization
T_0 = T[0,x]
#-----------------------------------
# Solve for the surface temperature
#-----------------------------------
# The 2m temperature and mixing ratio is taken from the
# boundary layer model (theta)
res = minimize(optim_T0,x0=T_0,args=(theta[1,x],q[1,x]/qsat[1,x],
albedo,G,p,rho,U,z,z0),bounds=((None,400),), \
method='L-BFGS-B',options={'eps':1e-8})
# Assign optimized surface temperature to the temperature array
T[0,x] = res.x
#-------------------------
# Solve the heat equation
#-------------------------
T = heat_equation_time_2D(T, dz, dt)
#-------------------------
# Solve the BL model
#-------------------------
# First, set the surface temperature from the soil module
theta[0,:] = T[0,:]
theta, q, qsat, rH, cov, adv, c, d, xa, za = boundary_layer_evolution_moisture(theta=theta,
q=q, u=U, K=0.5, dx=dx, dz=dza, Nx=Nx, Nz=Nza, dt=dt)
Task 6: Make some nice plots
# Create 2D plot for the covariance
ax = make_plot(theta, x=xa/1000, z=za, levels=11, title='Temperature', unit='K',
xlab='Distance [km]', zlab='Height [m]', cmap='RdBu_r')
ax = make_plot(T, x=xa/1000, z=np.arange(0, -Nz*dz, -dz), levels=11, title='Soil temperature', unit='K',
xlab='Distance [km]', zlab='Height [m]', cmap='RdBu_r')
# Create 2D plot for the covariance
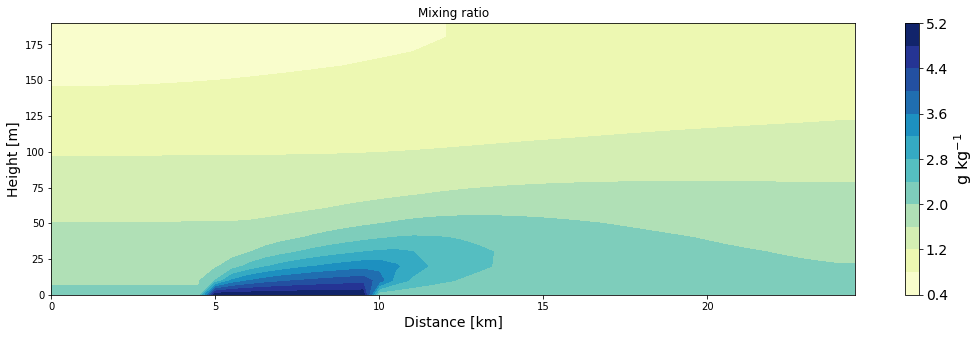
ax = make_plot(q, x=xa/1000, z=za, levels=11, title='Mixing ratio', unit='g kg$^{-1}$',
xlab='Distance [km]', zlab='Height [m]', cmap='YlGnBu')
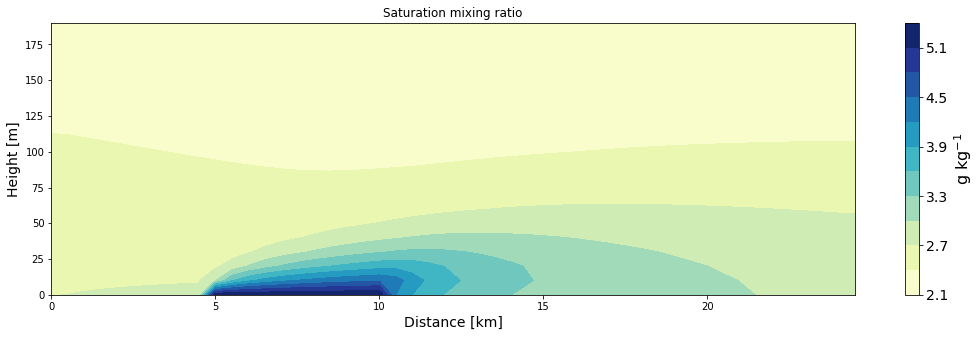
# Create 2D plot for the covariance
ax = make_plot(qsat, x=xa/1000, z=za, levels=11, title='Saturation mixing ratio', unit='g kg$^{-1}$',
xlab='Distance [km]', zlab='Height [m]', cmap='YlGnBu')
# Create 2D plot for the covariance
ax = make_plot(rH*100, x=xa/1000, z=za, levels=11, title='Relative humidity', unit='%',
xlab='Distance [km]', zlab='Height [m]', cmap='YlGnBu')
ax.contour(xa/1000, za, rH, levels=[0.95,1.0],colors='red');